ブール代数(Boolean algebra)
2種類の値(0,1)を使った代数体系です。ブール代数を使って論理関数を表現することができ、各種演算規則により論理の変換や圧縮を行うことができます。
- 交換則 a+b = b+a
- 結合則 a+(b+c) = (a+b)+c
- 吸収則 a・b+a = a
- 分配則 a・(b+c) = a・b+a・c
- ド・モルガンの定理 a・b = a + b
演習1 結合則
下記の結合則を確認する回路を作成し、判定方法も説明しなさい。
(a・b)・c = a・(b・c)
解説
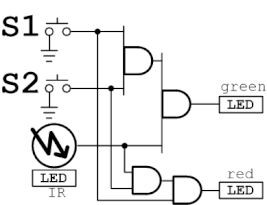
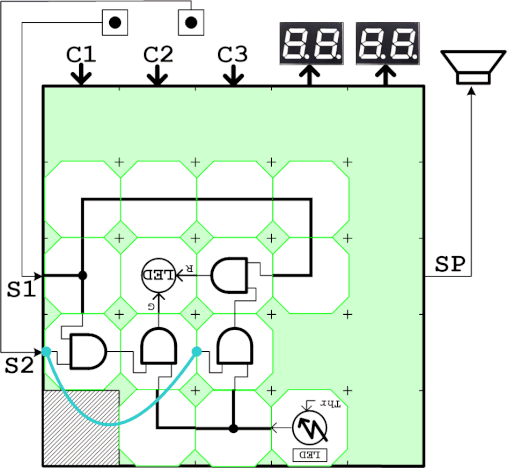
3つの入力a,b,cとして、それぞれスイッチS1,スイッチS2、近接センサを割り当てます。左辺の2つのANDからなる回路をブロックで実装してLEDの緑入力に接続します。また右辺の2つのANDからなる回路もブロックで実装しこちらはLEDの赤入力に接続します。
2つのスイッチと近接センサによって2^3=8通りの状態を作りLEDの緑と赤が同じように発光することを確認します。
回路図は以下のとおりです。
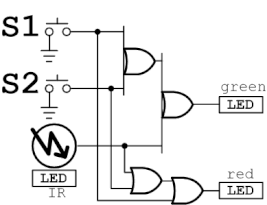
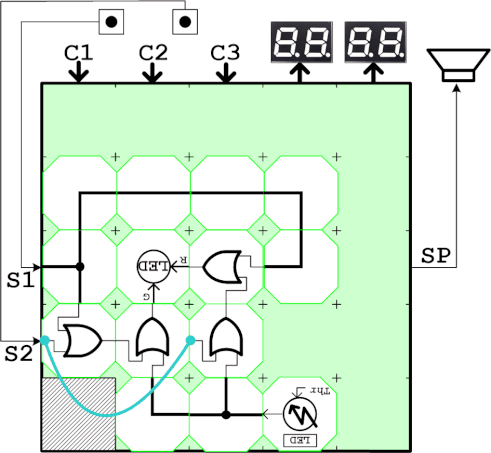
以下は補足ですが、OR演算による結合則
(a+b)+c = a+(b+c)
は、先の回路においてANDをORに置き換えるだけで確認ができます。
演習2 多入力AND演算
5入力AND回路を2入力ANDで作成し、出力の妥当性を確認する回路も併せて作りなさい。
解説
カウンタの出力の下位5bitを4つの2入力ANDゲートに入力し、最終出力はLEDに接続します。カウンタ下位5bitが全てHレベルの場合、つまりカウンタ値が1Fh,3Fh,5Fh,7Fh,9Fh,BFh,DFh,FFhの場合にLEDが点灯することを確認します。※通常の回路では8ビットカウンタ出力を直接ANDゲートに入力可能ですが、Cube-Dでは各ビットを分離するためにデコーダブロックが必要になります(シリアル通信でバス情報を送っているため)。
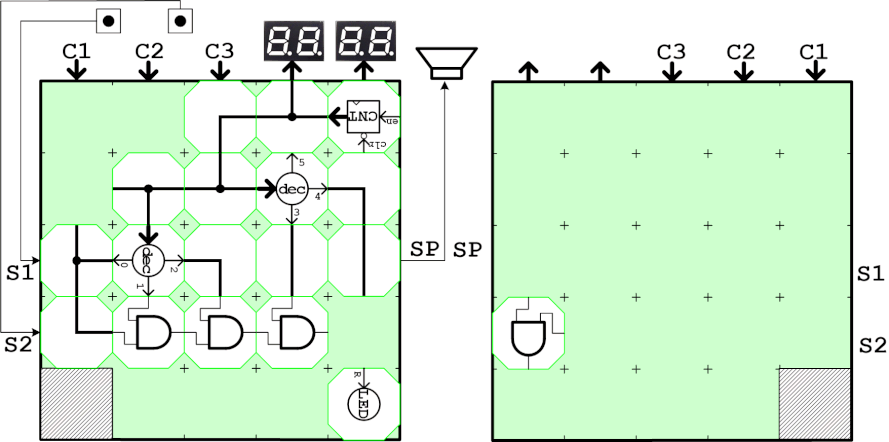
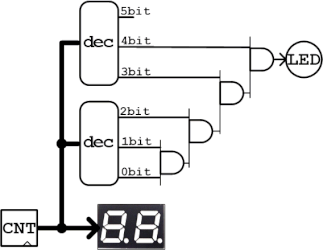
上記回路のANDをORに置き換えると、20h,40h,60h,80h,a0h,c0h,e0hでLEDが消灯する回路になります。併せて確認してみてください。
演習3 ド・モルガンの定理①
下記のド・モルガンの定理を確認する回路を作成、その確認方法も説明しなさい。
a・b = a + b
解説
2つの入力a,bとして、それぞれスイッチS1,スイッチS2を割り当てます。左辺の回路をブロックで実装してLEDの赤入力に接続します。また右辺の回路もブロックで実装しこちらはLEDの緑入力に接続します。NORブロックを使わずにORブロックとNOTブロックを使っているのは、ANDブロックとORブロックを入れ替えるだけでもう一つの式の確認もできるからです。
2つのスイッチより2^2=4通りの状態を作りLEDの緑と赤が同じタイミングで発光することを確認します。
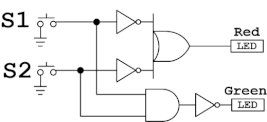
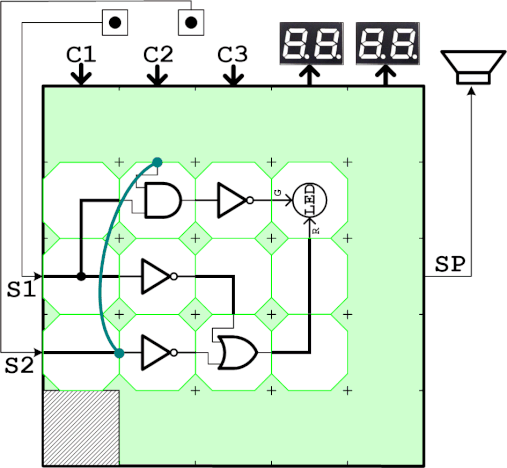
回路図は以下のとおりです。
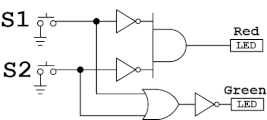
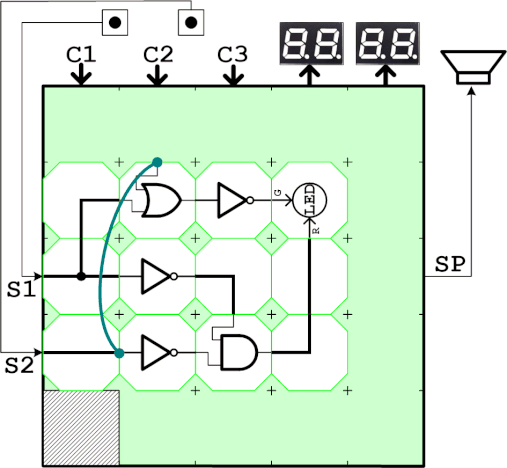
演習4 ド・モルガンの定理②
下記のド・モルガンの定理を確認する回路を作成、その確認方法も説明しなさい。
a+b = a・b
解説
演習3の回路においてANDブロックとORブロックのみを入れ替えてあります。確認方法等は同じです。
回路図は以下のとおりです。
演習5 完備性
N入力M出力の論理関数は、{AND,OR,NOT}の3基本関数の組み合わせで表現できる(完備性がある)が、NANDは完備性があることを示せ。
解説
NANDだけでAND,OR,NOTの3つと等価な論理が作り出せることを示します。
まずはNOTから。2入力を1つに束ねたものは、NANDの真理値表の入力00と11だけの表となり、NOTに一致することは明らかです。

NOT
続いてANDを作ってみます。
NANDの出力に先ほど確認したNOTを接続した回路なので明らかにANDになることが分かります。
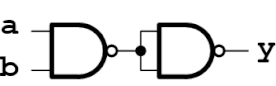
AND
最後はORです。
NANDの入力にNOTがそれぞれ接続されています。ド・モルガンの定理を使って変形します。
y = not( a・ b ) = a+b
ORになることが確認できました。以上でNANDは完備性があることが証明されました。
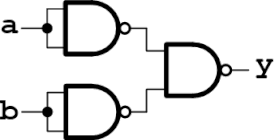
OR
XORをNANDだけで作成したらどのような回路になるでしょうか?
y = a・b+a・b
なので、先に求めたNOT, AND, ORを当てはめて変形すると5つのNANDで作ることができます。
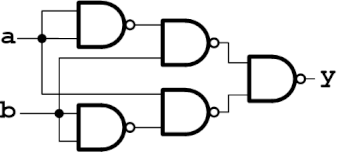
5つのNANDで構成したXOR
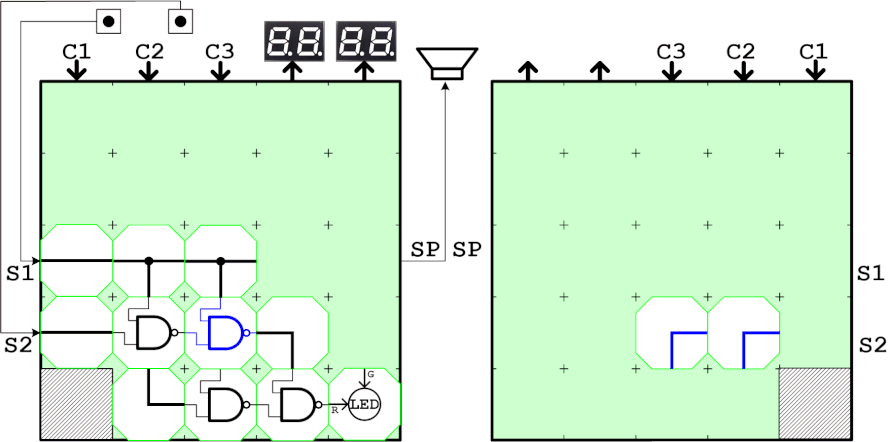
実はXORは4つのNANDで作ることができます。代数で変形するよりもCube-Dで回路を組んで真理値を確認したほうが早いので下のような回路を使って確認します。
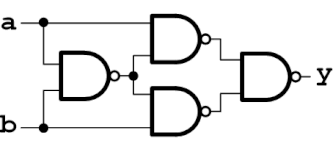
4つのNANDで構成したXOR
完備集合はその他に、{NOR},{AND,NOT},{OR,NOT}などがあります。
お知らせ
■2022/03/03-04 第20回たま工業交流展に出展予定でしたが、展示会自体がコロナのため中止となりました。
■2022/02/01 本店を神奈川県川崎市に移転しました。
■2021/07/19 「プログラミング学習装置」に関する特許が登録されました
■2021/01/20- バーチャル産業交流展に出展しました(1/20-2/19)。
■2020/12/26,27 Cube-D PGを使った「短期プログラミング教室」を開催しました。
■2020/08/25 ネットショップ用ページを追加しました。
■2020/08/11 クラウドファンディングの支援者様にCube-D PGを発送しました。
■2020/08/08 Cube-D PGの全マニュアル(組立、チュートリアル、詳細)を再度更新しました。
■2020/07/21 Cube-D PGの全マニュアル(組立、チュートリアル、詳細)を更新しました。
■2020/07/08 Cube-D PGのロボットカー組立マニュアルがダウンロードできるようになりました。
■2020/06/30 Cube-D PGのチュートリアルマニュアルがダウンロードできるようになりました。
■2020/06/15 「東京技術商店」にてCube-D PGの記事が掲載されました。
■2020/06/11 クラウドファンディング(未来ショッピング)で「Cube-D PG」を公開しました。
■2020/03/28 「プログラミング学習装置」の試作機が完成しました。
■2020/03/04 「プログラミング学習装置」に関する特許を出願しました。
■2019/11/13-15 産業交流展2019に出展しました。
■2019/10/09 ブロックシールPDFがダウンロードできるようになりました。
■2019/09/12 2ブロックだけで作る回路例20を追加しました。
■2019/09/07 Cube-Dを使った論理回路実験室を追加しました。
■2019/09/03 楽天、Yahoo、ヤマダモールでCube-Dとデジタルパペットの販売を開始しました。
■2019/08/09 未来ショッピング公式ストアでCube-Dの販売を開始しました。
■2019/07/19 Makuakeストアからデジタルパペットが購入できるようになりました。
■2019/06/14 デジタルパペットのCFは目標金額の128%で終了しました。ペーパークラフトを公開しました。
■2019/05/22 デジタルパペットの取扱説明書をアップロードしました。
■2019/04/22 Makuake(クラウドファンディング)で「デジタルパペット」を公開しました。
■2019/02/03 アカデミックセット25の一般販売を開始しました(Amazon)。
■2019/01/14 アカデミック版対応操作マニュアル。回路集100をアップロードしました。
■2019/01/14 Cube-D事業を株式会社デジタルキューブに移管しました。

株式会社デジタルキューブ
〒210-0007 神奈川県川崎市川崎区駅前本町11番地2 川崎フロンティアビル4F
電話/FAX 044-813-4547 E-mail info@cube-d.co.jp
